Game Theory X Reinforcement Learning(From Scratch)

写在前面

强化学习与博弈论本身可以说是两个独立的学科，一个源于经济学、数学，另一个源于机器学习、控制论，但两者之间有非常紧密的联系，你可能会发现一些概念和术语都存在重叠，比如：

1. 策略（Strategy/Policy）：

• 博弈论研究参与者在特定信息结构下的策略选择；
• 强化学习中，智能体学习的是“策略”函数 $\pi$ ：给定状态下采取哪个动作；

2. 回报函数 / 奖励函数：

• 博弈论中，玩家有效用函数（utility function）；
• RL 中，智能体有奖励函数（reward function）；

虽然两者存在一定的交集，特别是在 多智能体强化学习（Multi-Agent RL, MARL） 方面，但注意一些概念并不完全等价，一个随机博弈可以看成是一个多智能体强化学习过程，但是：

• 随机博弈中，假定每个玩家都是完全理性的，并且已知博弈结构（即每个状态的奖励矩阵是已知的，不需要学习）；
• 多智能体强化学习是通过交互学习，并不知道环境或他人策略，通过与环境的不断交互来学习每个状态的奖励值函数，再通过这些奖励值函数来学习得到最优纳什策略或其他策略函数。需要利用 Q-learning 及其扩展方法来不断逼近逼近状态值函数 $V(s)$ 或动作-状态值函数 $Q(s, a)$ ；

博弈论为研究多智能体系统及开发具有良好理论特性和收敛保证的 MARL 算法提供了有力工具。

至于单智能体的强化学习，能否将其视为 agent vs. environment 的博弈，个人认为至少从博弈论的视角理解是不太对的，因为博弈论中，对手应该是理性、反应型的玩家，而强化学习中，环境不主动策略反应，并且策略中并不存在耦合。

单智能体的强化学习更偏向于决策论（研究玩家在给定其他环境参数条件下的最优选择问题，并且策往往会带来“后果”，因此决策者需要为未来负责，在未来的时间点做出进一步的决策）。

而传统的机器学习就是预测，仅仅产生一个针对输入数据的信号，并期望它和未来可观测到的信号一致。

一、博弈论相关预备知识速通

1.1 Game Representations（博弈表示）

1.1.1 博弈要素

• Players 参与者；
• Strategies 策略；
  • $s_i$: $Player_i$ 的某个特定策略；
  • $S_i$: $Player_i$ 的策略集合；
  • $S$: 一次博弈，即所有参与者的策略组合；
  • $S_{-i}$: 一次博弈中除了 $Player_i$ 之外的其他所有参与者的策略；
• Payoff 收益；
• Assumption 假设：每个参与者都知道其他人的可能策略和收益，即博弈者之间信息透明；

1.1.2 博弈形式

描述博弈有 2 种不同的方式：

1. Normal Form Game（正则/标准形式的博弈）：也叫战略形式博弈（Strategic Form Game），适合一次性、同时选择策略的博弈。
   • 所有玩家同时选择策略；
   • 不考虑行动顺序；
   • 用一个博弈矩阵列出所有可能的策略组合及对应的收益；

经典的囚徒困境就属于这种形式，其博弈矩阵如下：

	对方沉默	对方坦白
你沉默	(-1,-1)	(-10, 0)
你坦白	(0, -10)	(-5,-5)

2. Extensive Form Game（扩展形式的博弈）：也叫博弈树形式，适合描述具有决策顺序、信息结构和动态变化的博弈。
   • 行动按顺序进行；
   • 具有信息集（用于表示不完全信息）、博弈树、博弈节点；
   • 可以表达“谁先动”、“谁观察到什么”等信息；（可以有完美信息或不完全信息）
   • 更适合分析动态博弈、有先后顺序的博弈、非完全信息博弈；

Sequential games（序贯博弈） 是扩展形式的一个子集，一种情形如下：

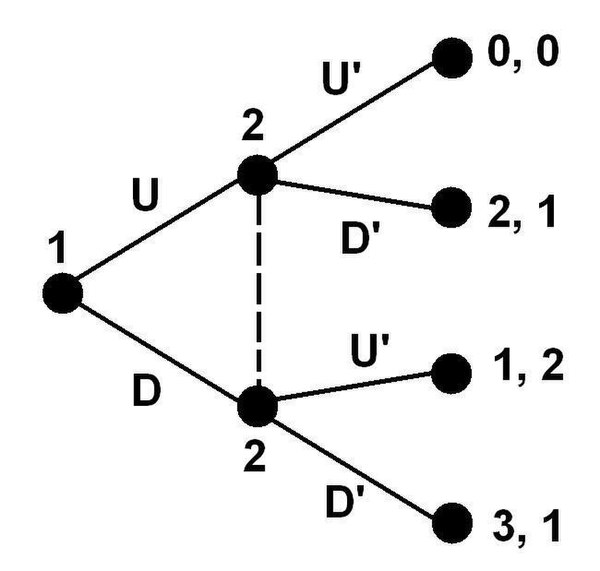
在这个博弈树中，虚线连接了玩家 2 的两个决策节点，构成了一个信息集，参与者无法区分信息集里的多个节点。也就是说：如果信息集有多个节点，信息集所属的参与者就不知道能往哪个节点移动。

所以，当玩家2 做决策（选择 $U^\prime$ 或 $D^\prime$ ）时，他不知道自己是在上面的节点还是下面的节点，即他不知道玩家1 之前是选了 $U$ 还是 $D$ 。这就是不完美信息。

1.2 Classification of Games（博弈分类）

Simultaneous games （同时博弈/策略博弈）：双方同时行动的博弈，或者如果双方不同时行动，后行动者对先行动者的行为一无所知（使其实际上等同于同时行动）。通常使用正则形式来表示同时博弈。	Sequential games（序贯博弈）：指后行动者对先行动者的行为有一定了解的游戏。通常使用扩展形来表示序贯博弈。
Cooperative games（合作博弈）：参与者能够形成具有约束力的外部承诺的博弈（例如通过合同法强制执行），不能只是口头上的约定。	Non-cooperative games（非合作博弈）：参与者无法形成联盟，由于缺乏执行合作行为的外部手段（例如合同法），只有自我实施（例如通过可靠的威胁）联盟是可能的。
Zero-sum games（零和博弈）：每个参与者的效用收益或损失恰好被其他参与者的效用损失或收益所平衡的博弈。	Non-zero-sum games（非零和博弈）：相互作用方的总收益和损失可以小于或大于零的博弈。
Perfect information games（完美信息博弈）：指所有参与者都了解其他参与者先前采取的行动的博弈。	Imperfect information games（不完美信息博弈）：部分参与者不了解其他参与者先前采取的行动的博弈。
Complete information games （完全信息博弈）：指所有参与者都了解其他参与者可用的策略和收益的博弈。	Incomplete information games（不完全信息博弈）：指部分参与者不了解其他参与者可用的策略或收益的博弈。
Finite games（有限博弈）：持续有限步数的博弈。	Infinite games（无限博弈）：重复或持续无限步数的博弈。

1.3 Nash Equilibrium（纳什均衡）