写在前面
变分信息瓶颈(Variational Information Bottleneck,VIB),简单来说,可视为一种正则化方法,用于引导模型只保留必要信息 ,压缩冗余,预测准确。本文参考了经典论文 《Deep Variational Information Bottleneck》 ,勉强也算是论文阅读笔记吧,不过只摘录了推导部分以及结合了个人的理解,没有放具体的实验效果。
一、预备知识
信息量 :用来消除随机不确定性,信息发生的概率越小,即不确定性越大,信息量越小 。设某事件 x x x p ( x ) p(x) p ( x ) I ( x ) = − log p ( x ) I(x) = -\log p(x) I ( x ) = − log p ( x )
信息单位:用 2 2 2 比特(bit) ,可以简单理解为用多少个比特可以表示这个变量;用 e e e nat 。
信息熵 Entropy :用来表示信息的平均不确定度 ,若一个离散随机变量 X X X { x 1 , x 2 , … , x n } \{x_1, x_2, \dots, x_n\} { x 1 , x 2 , … , x n } p ( x ) p(x) p ( x ) H ( X ) = − ∑ i p ( x i ) log p ( x i ) H(X) = - \sum_{i} p(x_i) \log p(x_i) H ( X ) = − ∑ i p ( x i ) log p ( x i )
条件熵 Conditional Entropy :用来表示知道另一个变量后剩下的不确定性 。设 X X X Y Y Y H ( Y ∣ X ) = E x ∼ p ( x ) [ H ( Y ∣ X = x ) ] H(Y|X) = \mathbb{E}_{x \sim p(x)} [H(Y|X = x)] H ( Y ∣ X ) = E x ∼ p ( x ) [ H ( Y ∣ X = x )] X X X Y Y Y
互信息 Mutual Information :用来表示两个变量间共享的信息 。它衡量的是已知随机变量 X X X Y Y Y X X X Y Y Y
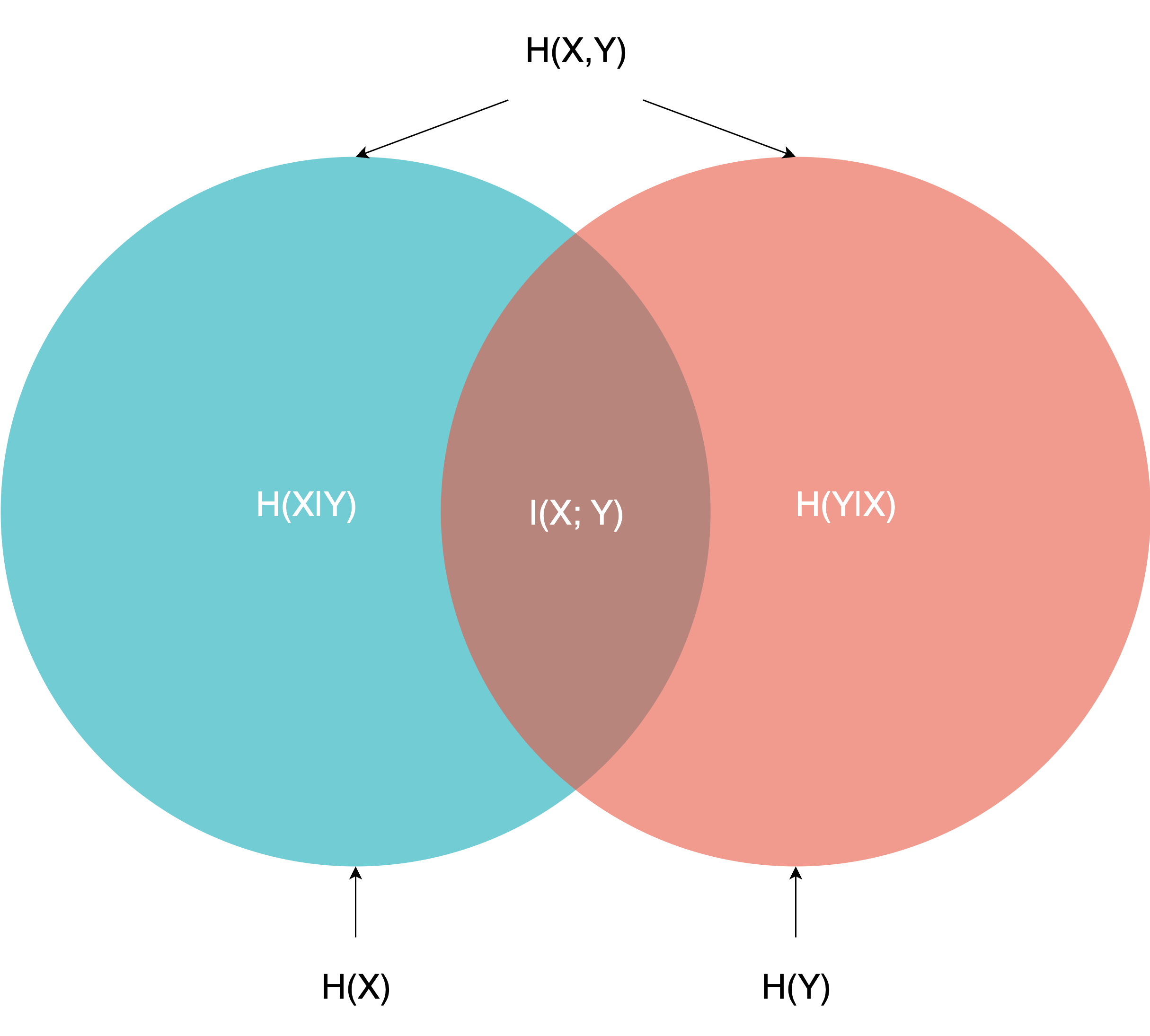
其中,I ( X ; Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) − H ( X ∣ Y ) I(X; Y) = H(Y) - H(Y|X) = H(X) - H(X|Y) I ( X ; Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) − H ( X ∣ Y )
或者也可以写为 I ( X ; Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X; Y) = H(X) + H(Y) - H(X, Y) I ( X ; Y ) = H ( X ) + H ( Y ) − H ( X , Y )
用概率代入可得:I ( X ; Y ) = ∑ x , y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) I(X; Y) = \sum_{x,y} p(x, y) \log \frac{p(x, y)}{p(x)p(y)} I ( X ; Y ) = ∑ x , y p ( x , y ) log p ( x ) p ( y ) p ( x , y )
若两个变量相互独立,显然互信息为 0 。
相对熵(KL 散度,Kullback-Leibler Divergence) :用来表示两个概率分布的差异 。如果对于随机变量 X X X P ( X ) P(X) P ( X ) Q ( X ) Q(X) Q ( X ) D K L ( P ∣ ∣ Q ) = − ∑ x P ( x ) ln Q ( x ) P ( x ) = ∑ x P ( x ) ln P ( x ) Q ( x ) D_{KL}(P || Q) = - \sum_x P(x) \ln \frac{Q(x)}{P(x)} = \sum_x P(x) \ln \frac{P(x)}{Q(x)} D K L ( P ∣∣ Q ) = − ∑ x P ( x ) ln P ( x ) Q ( x ) = ∑ x P ( x ) ln Q ( x ) P ( x )
写成上面那种形式可能并不太方便理解和记忆,D K L ( P ∣ ∣ Q ) = ∑ x P ( x ) ln P ( X ) − P ( X ) ln Q ( X ) D_{KL}(P || Q) = \sum_xP(x)\ln{P(X)} - P(X)\ln{Q(X)} D K L ( P ∣∣ Q ) = ∑ x P ( x ) ln P ( X ) − P ( X ) ln Q ( X ) P P P 信息熵 ,第二部分是 Q Q Q P P P 交叉熵 ,所以 KL 散度可以简单理解为,站在 P P P Q Q Q P P P 。
一些特性:
D K L ( P ∣ ∣ Q ) ≥ 0 D_{KL}(P || Q) \ge 0 D K L ( P ∣∣ Q ) ≥ 0 P ( X ) = Q ( X ) P(X) = Q(X) P ( X ) = Q ( X ) D K L ( P ∣ ∣ Q ) ≠ D K L ( Q ∣ ∣ P ) D_{KL}(P||Q) \neq D_{KL}(Q||P) D K L ( P ∣∣ Q ) = D K L ( Q ∣∣ P ) 不是一个真正的度量或距离 ;
交叉熵(Cross Entropy) :主要用于衡量两个概率分布之间的差异,定义为:H ( p , q ) = − ∑ x p ( x ) log q ( x ) H(p, q) = - \sum_x p(x) \log q(x) H ( p , q ) = − ∑ x p ( x ) log q ( x ) 交叉熵 = 信息熵 + KL 散度 ,那么,KL 散度其实就是交叉熵和真实熵之间的“差距” ;
既然交叉熵和 KL 散度都是用来衡量两个概率分布的差异性,那么他们有什么区别呢?
交叉熵 vs. KL 散度 :在监督学习中,或是训练神经网络时:
p(x):表示真实分布(通常是 one-hot 标签) q(x):是模型输出的概率分布(softmax 后) 通常会用交叉熵作为 loss function ,目标就是 Minimize H ( p , q ) H(p,q) H ( p , q ) ⇔ \Leftrightarrow ⇔ D K L D_{KL} D K L H ( p ) H(p) H ( p ) 最小化 KL 散度 ,不过因为 KL 散度需要额外计算信息熵,所以常用交叉熵。
二、关于信息瓶颈理论
2.1 信息瓶颈 IB
在深度学习中,信息瓶颈理论事实上就是把神经网络理解为一个编码器和解码器,设:
X X X Y Y Y Z Z Z X X X X X X Z Z Z
神经网络结构如下:
X → Z → Y X \rightarrow Z \rightarrow Y
X → Z → Y
IB 的核心目标就是,在保留与输出 Y Y Y X X X Z Z Z
Z Z Z X X X Z Z Z Y Y Y
可以用数学语言描述如下:
R I B ( θ ) = I ( Z ; Y ; θ ) − β I ( Z ; X ; θ ) R_{IB}(\theta)=I(Z;Y;\theta)-\beta I(Z;X;\theta)
R I B ( θ ) = I ( Z ; Y ; θ ) − β I ( Z ; X ; θ )
其中:
β \beta β θ \theta θ
所以,训练的目标就是要最大化 Z Z Z Y Y Y Z Z Z X X X 。
2.2 变分信息瓶颈 VIB
优化的目标包含两个互信息,先对两个互信息进行展开,
I ( Z ; Y ) = ∫ p ( y , z ) log p ( y , z ) p ( y ) p ( z ) d y d z = ∫ p ( y , z ) log p ( y ∣ z ) p ( y ) d y d z \begin{aligned}
I(Z;Y)&=\int p(y,z)\log{\frac{p(y,z)}{p(y)p(z)}}\,dy\,dz\\
&=\int p(y,z)\log{\frac{p(y|z)}{p(y)}}\,dy\,dz
\end{aligned}
I ( Z ; Y ) = ∫ p ( y , z ) log p ( y ) p ( z ) p ( y , z ) d y d z = ∫ p ( y , z ) log p ( y ) p ( y ∣ z ) d y d z
I ( X ; Z ) = ∫ p ( z , x ) log p ( z , x ) p ( z ) p ( x ) d z d x = ∫ p ( z , x ) log p ( z ∣ x ) p ( z ) d z d x \begin{aligned}
I(X;Z)&=\int p(z,x)\log{\frac{p(z,x)}{p(z)p(x)}}\,dz\,dx\\
&=\int p(z,x)\log{\frac{p(z|x)}{p(z)}}\,dz\,dx
\end{aligned}
I ( X ; Z ) = ∫ p ( z , x ) log p ( z ) p ( x ) p ( z , x ) d z d x = ∫ p ( z , x ) log p ( z ) p ( z ∣ x ) d z d x
2.2.1 模型假设
我们先给出 VIB 建模的核心假设:
Y ↔ X ↔ Z Y \leftrightarrow X \leftrightarrow Z
Y ↔ X ↔ Z
即马尔可夫链假设 ,其直观意义是:Y Y Y Z Z Z X X X Z Z Z X X X Y Y Y
p ( z ∣ x , y ) = p ( z ∣ x ) p(z|x,y)=p(z|x)
p ( z ∣ x , y ) = p ( z ∣ x )
也可以从任务的角度理解:
模型结构中,Z Z Z X X X
我们没有直接从 Y Y Y Z Z Z ,而是由 X X X Z Z Z
基于该假设,联合分布可以分解为:
p ( X , Y , Z ) = p ( X ) ⋅ p ( Y ∣ X ) ⋅ p ( Z ∣ X , Y ) (链式法则) = p ( X ) ⋅ p ( Y ∣ X ) ⋅ p ( Z ∣ X ) (马尔可夫链性质) \begin{aligned}
p(X, Y, Z) &= p(X) \cdot p(Y|X) \cdot p(Z|X, Y) \quad \text{(链式法则)}\\
&= {p(X) \cdot p(Y|X) \cdot p(Z|X)} \quad \text{(马尔可夫链性质)}
\end{aligned}
p ( X , Y , Z ) = p ( X ) ⋅ p ( Y ∣ X ) ⋅ p ( Z ∣ X , Y ) ( 链式法则 ) = p ( X ) ⋅ p ( Y ∣ X ) ⋅ p ( Z ∣ X ) ( 马尔可夫链性质 )
其中:
p ( X ) p(X) p ( X ) p ( Y ∣ X ) p(Y|X) p ( Y ∣ X ) p ( Z ∣ X ) p(Z|X) p ( Z ∣ X )
再看后验分布 p ( y ∣ z ) p(y|z) p ( y ∣ z )
p ( y ∣ z ) = ∫ p ( x , y ∣ z ) d x = ∫ p ( y ∣ x ) ⋅ p ( x ∣ z ) d x = ∫ p ( z ∣ x ) p ( x , y ) p ( z ) d x = ∫ p ( y ∣ x ) ⋅ p ( z ∣ x ) p ( x ) p ( z ) d x \begin{aligned}
p(y|z) &= \int p(x, y | z) \,dx \\
&= \int p(y|x) \cdot p(x|z) \,dx \\
&= \int \frac{p(z|x) p(x, y)}{p(z)} \,dx \\
&= \int p(y|x) \cdot \frac{p(z|x)p(x)}{p(z)} \,dx
\end{aligned}
p ( y ∣ z ) = ∫ p ( x , y ∣ z ) d x = ∫ p ( y ∣ x ) ⋅ p ( x ∣ z ) d x = ∫ p ( z ) p ( z ∣ x ) p ( x , y ) d x = ∫ p ( y ∣ x ) ⋅ p ( z ) p ( z ∣ x ) p ( x ) d x
可以发现,p ( y ∣ z ) p(y|z) p ( y ∣ z ) p ( z ∣ x ) p(z|x) p ( z ∣ x ) p ( y ∣ z ) p(y|z) p ( y ∣ z )
2.2.2 互信息 I ( Z ; Y ) I(Z;Y) I ( Z ; Y )
后验概率 p ( y ∣ z ) p(y|z) p ( y ∣ z ) 解码器(decoder) q ϕ ( y ∣ z ) q_\phi(y|z) q ϕ ( y ∣ z ) p ( y ∣ z ) p(y|z) p ( y ∣ z )
利用 KL 散度的非负性质:
D K L ( p ( y ∣ z ) ∣ ∣ q ( y ∣ z ) ) ≥ 0 ⇒ ∫ p ( y ∣ z ) log p ( y ∣ z ) ≥ ∫ p ( y ∣ z ) log q ( y ∣ z ) \begin{aligned}
& D_{KL}(p(y|z)||q(y|z))\ge 0 \\
\Rightarrow & \int p(y|z)\log{p(y|z)} \ge \int p(y|z)\log{q(y|z)}\\
\end{aligned}
⇒ D K L ( p ( y ∣ z ) ∣∣ q ( y ∣ z )) ≥ 0 ∫ p ( y ∣ z ) log p ( y ∣ z ) ≥ ∫ p ( y ∣ z ) log q ( y ∣ z )
则有:
I ( Z ; Y ) = ∫ p ( y , z ) log p ( y ∣ z ) p ( y ) d y d z ≥ ∫ p ( y , z ) log q ( y ∣ z ) d y d z − ∫ p ( y , z ) log p ( y ) d y d z = ∫ p ( y , z ) log q ( y ∣ z ) d y d z + H ( Y ) \begin{aligned}
I(Z;Y) & =\int p(y,z)\log{\frac{p(y|z)}{p(y)}}\,dy\,dz \\
& \ge \int p(y,z)\log{q(y|z)}\,dy\,dz - \int p(y,z)\log{p(y)}\,dy\,dz\\
& = \int p(y,z)\log{q(y|z)}\,dy\,dz + H(Y)
\end{aligned}
I ( Z ; Y ) = ∫ p ( y , z ) log p ( y ) p ( y ∣ z ) d y d z ≥ ∫ p ( y , z ) log q ( y ∣ z ) d y d z − ∫ p ( y , z ) log p ( y ) d y d z = ∫ p ( y , z ) log q ( y ∣ z ) d y d z + H ( Y )
其中 H ( Y ) H(Y) H ( Y ) y y y
I ( Z ; Y ) ≥ ∫ p ( y , z ) log q ( y ∣ z ) d y d z I(Z;Y)\ge \int p(y,z)\log{q(y|z)}\,dy\,dz
I ( Z ; Y ) ≥ ∫ p ( y , z ) log q ( y ∣ z ) d y d z
对于 p ( y , z ) p(y,z) p ( y , z )
p ( y , z ) = ∫ p ( x , y , z ) d x = ∫ p ( x ) ⋅ p ( y ∣ x ) ⋅ p ( z ∣ x ) d x \begin{aligned}
p(y,z)&=\int p(x,y,z)\, dx\\
&=\int p(x) \cdot p(y|x) \cdot p(z|x)\,dx \\
\end{aligned}
p ( y , z ) = ∫ p ( x , y , z ) d x = ∫ p ( x ) ⋅ p ( y ∣ x ) ⋅ p ( z ∣ x ) d x
所以,下界可以写为:
I ( Z ; Y ) ≥ ∫ p ( x ) ⋅ p ( y ∣ x ) ⋅ p ( z ∣ x ) log q ( y ∣ z ) d x d y d z I(Z;Y)\ge \int p(x)\cdot p(y|x)\cdot p(z|x)\log{q(y|z)}\,dx\,dy\,dz
I ( Z ; Y ) ≥ ∫ p ( x ) ⋅ p ( y ∣ x ) ⋅ p ( z ∣ x ) log q ( y ∣ z ) d x d y d z
2.2.3 互信息 I ( X , Z ) I(X,Z) I ( X , Z )
I ( X ; Z ) = ∫ p ( z , x ) log p ( z ∣ x ) p ( z ) d z d x = ∫ p ( z , x ) log p ( z ∣ x ) d z d x − ∫ p ( z , x ) log p ( z ) d z d x \begin{aligned}
I(X;Z)&=\int p(z,x)\log{\frac{p(z|x)}{p(z)}}\,dz\,dx \\
&=\int p(z,x)\log{p(z|x)}\,dz\,dx-\int p(z,x)\log{p(z)}\,dz\,dx \\
\end{aligned}
I ( X ; Z ) = ∫ p ( z , x ) log p ( z ) p ( z ∣ x ) d z d x = ∫ p ( z , x ) log p ( z ∣ x ) d z d x − ∫ p ( z , x ) log p ( z ) d z d x
p ( z , x ) p(z,x) p ( z , x ) p ( z ∣ x ) ⋅ p ( x ) p(z|x)\cdot p(x) p ( z ∣ x ) ⋅ p ( x ) p ( z ) p(z) p ( z ) p ( z ) = ∫ p ( z ∣ x ) p ( x ) d x p(z)=\int p(z|x)p(x)\,dx p ( z ) = ∫ p ( z ∣ x ) p ( x ) d x r ( z ) r(z) r ( z ) p ( z ) p(z) p ( z )
D K L ( p ( z ) ∣ ∣ r ( z ) ) ≥ 0 ⇒ ∫ p ( z ) log p ( z ) ≥ ∫ p ( z ) log r ( z ) \begin{aligned}
& D_{KL}(p(z)||r(z))\ge 0 \\
\Rightarrow & \int p(z)\log{p(z)} \ge \int p(z)\log{r(z)}\\
\end{aligned}
⇒ D K L ( p ( z ) ∣∣ r ( z )) ≥ 0 ∫ p ( z ) log p ( z ) ≥ ∫ p ( z ) log r ( z )
则有:
I ( X ; Z ) = ∫ p ( z , x ) log p ( z ∣ x ) d z d x − ∫ p ( z , x ) log p ( z ) d z d x ≤ ∫ p ( z , x ) log p ( z ∣ x ) d z d x − ∫ p ( z , x ) log r ( z ) d z d x = ∫ p ( z ∣ x ) ⋅ p ( x ) ⋅ log p ( z ∣ x ) r ( z ) d z d x \begin{aligned}
I(X;Z)&=\int p(z,x)\log{p(z|x)}\,dz\,dx-\int p(z,x)\log{p(z)}\,dz\,dx \\
&\le \int p(z,x)\log{p(z|x)}\,dz\,dx-\int p(z,x)\log{r(z)}\,dz\,dx \\
&=\int p(z|x)\cdot p(x)\cdot \log{\frac{p(z|x)}{r(z)}}\,dz\,dx
\end{aligned}
I ( X ; Z ) = ∫ p ( z , x ) log p ( z ∣ x ) d z d x − ∫ p ( z , x ) log p ( z ) d z d x ≤ ∫ p ( z , x ) log p ( z ∣ x ) d z d x − ∫ p ( z , x ) log r ( z ) d z d x = ∫ p ( z ∣ x ) ⋅ p ( x ) ⋅ log r ( z ) p ( z ∣ x ) d z d x
2.2.4 变分信息瓶颈下界
结合以上推导的最终结果,可以得到:
R I B = I ( Z ; Y ) − β I ( Z ; X ) ≥ ∫ p ( x ) ⋅ p ( y ∣ x ) ⋅ p ( z ∣ x ) log q ( y ∣ z ) d x d y d z − β ∫ p ( z ∣ x ) ⋅ p ( x ) ⋅ log p ( z ∣ x ) r ( z ) d z d x \begin{aligned}
R_{IB}&=I(Z;Y)-\beta I(Z;X)\\
&\ge \int p(x)\cdot p(y|x)\cdot p(z|x)\log{q(y|z)}\,dx\,dy\,dz - \beta\int p(z|x)\cdot p(x)\cdot \log{\frac{p(z|x)}{r(z)}}\,dz\,dx \\
\end{aligned}
R I B = I ( Z ; Y ) − β I ( Z ; X ) ≥ ∫ p ( x ) ⋅ p ( y ∣ x ) ⋅ p ( z ∣ x ) log q ( y ∣ z ) d x d y d z − β ∫ p ( z ∣ x ) ⋅ p ( x ) ⋅ log r ( z ) p ( z ∣ x ) d z d x
将下界记为 L \mathcal{L} L
我们用经验分布来代替真实分布 ,即我们在不知道真实分布 p ( x ) p(x) p ( x ) p ( y ) p(y) p ( y ) p ( x , y ) p(x,y) p ( x , y )
设我们有 N N N { ( x n , y n ) } n = 1 N \{(x_n, y_n)\}_{n=1}^N {( x n , y n ) } n = 1 N
对于 x x x p ^ ( x ) = 1 N ∑ n = 1 N δ x n ( x ) \widehat{p}(x) = \frac{1}{N} \sum_{n=1}^N \delta_{x_n}(x) p ( x ) = N 1 ∑ n = 1 N δ x n ( x )
对于 y y y p ^ ( y ) = 1 N ∑ n = 1 N δ y n ( y ) \widehat{p}(y) = \frac{1}{N} \sum_{n=1}^N \delta_{y_n}(y) p ( y ) = N 1 ∑ n = 1 N δ y n ( y )
对于联合分布 ( x , y ) (x, y) ( x , y ) p ^ ( x , y ) = 1 N ∑ n = 1 N δ ( x n , y n ) ( x , y ) \widehat{p}(x, y) = \frac{1}{N} \sum_{n=1}^N \delta_{(x_n, y_n)}(x, y) p ( x , y ) = N 1 ∑ n = 1 N δ ( x n , y n ) ( x , y )
其中 δ x n ( x ) \delta_{x_n}(x) δ x n ( x ) 狄拉克 delta 函数 ,表示一个“把质量全部放在样本点 x n x_n x n
δ x n ( x ) = { + ∞ x = x n 0 x ≠ x n , ∫ δ x n ( x ) d x = 1 \delta_{x_n}(x) = \begin{cases} +\infty & x = x_n \\ 0 & x \ne x_n \end{cases} ,\quad \int \delta_{x_n}(x) dx = 1
δ x n ( x ) = { + ∞ 0 x = x n x = x n , ∫ δ x n ( x ) d x = 1
如果不太好理解,你也可以当成直接把概率积分改成离散样本的求和取平均,总之有:
L = 1 N ∑ n = 1 N [ ∫ p ( z ∣ x n ) log q ( y n ∣ z ) − β p ( z ∣ x n ) log p ( z ∣ x n ) r ( z ) d z ] \mathcal{L}=\frac{1}{N}\sum_{n=1}^N\left[\int {p(z|x_n)\log{q(y_n|z)}- \beta p(z|x_n)\log{\frac{p(z|x_n)}{r(z)}}}\,dz\right]
L = N 1 n = 1 ∑ N [ ∫ p ( z ∣ x n ) log q ( y n ∣ z ) − βp ( z ∣ x n ) log r ( z ) p ( z ∣ x n ) d z ]
如果编码器(Encoder)是类似 VAE 的结构:
Variational Autoencoder(VAE)是一种生成模型,它学习数据 x x x z z z z z z 重新生成数据 。
神经网络是“可导”的函数,但是采样操作是不可导的,VAE 使用了重参数技巧(Reparameterization Trick) ,首先,给定样本 x n x_n x n p ( z ∣ x n ) = N ( z ∣ f e μ ( x n ) , f e Σ ( x n ) ) p(z|x_n) = \mathcal{N}(z|f_e^\mu(x_n), f_e^\Sigma(x_n)) p ( z ∣ x n ) = N ( z ∣ f e μ ( x n ) , f e Σ ( x n ))
均值:f μ ( x n ) f_\mu(x_n) f μ ( x n )
协方差(或标准差):f e Σ ( x n ) f_e^\Sigma(x_n) f e Σ ( x n )
f e f_e f e
然后将随机变量的“采样”过程拆成“可导的函数 + 固定随机数”:
z = f ( x n , ϵ ) = f e Σ ( x n ) ⋅ ϵ + f e μ ( x n ) , ϵ ∼ N ( 0 , 1 ) z = f(x_n, \epsilon) = f_e^\Sigma(x_n) \cdot \epsilon + f_e^\mu(x_n), \quad \epsilon \sim \mathcal{N}(0, 1)
z = f ( x n , ϵ ) = f e Σ ( x n ) ⋅ ϵ + f e μ ( x n ) , ϵ ∼ N ( 0 , 1 )
那么,最大化信息瓶颈等价于最小化:
J I B = 1 N ∑ n = 1 N E ϵ ∼ N ( 0 , 1 ) [ − log q ( y n ∣ f ( x n , ϵ ) ) ] + β D K L ( p ( z ∣ x , n ) ∣ ∣ r ( z ) ) J_{IB}=\frac{1}{N}\sum_{n=1}^N \mathbb{E}_{\epsilon \sim \mathcal{N}(0, 1)}\left[-\log{q(y_n|f(x_n,\epsilon))}\right ] +\beta D_{KL}(p(z|x,n)||r(z))
J I B = N 1 n = 1 ∑ N E ϵ ∼ N ( 0 , 1 ) [ − log q ( y n ∣ f ( x n , ϵ )) ] + β D K L ( p ( z ∣ x , n ) ∣∣ r ( z ))
三、个人的一些理解
在变分信息瓶颈(VIB)中,我们把输入 x n x_n x n p ( z ∣ x n ) p(z|x_n) p ( z ∣ x n )
一方面想让所有 p ( z ∣ x n ) p(z|x_n) p ( z ∣ x n )
另一方面又希望保留足够信息使得从 z ∼ p ( z ∣ x n ) z \sim p(z|x_n) z ∼ p ( z ∣ x n ) y n y_n y n
这与我们上面推导出的优化目标是一致的,即:
J I B = 1 N ∑ n = 1 N E ϵ ∼ N ( 0 , 1 ) [ − log q ( y n ∣ f ( x n , ϵ ) ) ] ⏟ 预测损失 + β D K L ( p ( z ∣ x , n ) ∣ ∣ r ( z ) ) ⏟ 压缩信息 J_{IB}=\frac{1}{N}\sum_{n=1}^N \underbrace{\mathbb{E}_{\epsilon \sim \mathcal{N}(0, 1)}\left[-\log{q(y_n|f(x_n,\epsilon))}\right ]}_{\text{预测损失}} + \underbrace{\beta D_{KL}(p(z|x,n)||r(z))}_{\text{压缩信息}}
J I B = N 1 n = 1 ∑ N 预测损失 E ϵ ∼ N ( 0 , 1 ) [ − log q ( y n ∣ f ( x n , ϵ )) ] + 压缩信息 β D K L ( p ( z ∣ x , n ) ∣∣ r ( z ))
其中,KL 项的惩罚促使不同输入 x n x_n x n p ( z ∣ x n ) p(z|x_n) p ( z ∣ x n ) r ( z ) r(z) r ( z ) N ( 0 , 1 ) \mathcal{N}(0, 1) N ( 0 , 1 ) z z z y y y q ( y ∣ z ) q(y|z) q ( y ∣ z ) z z z y y y x x x y y y
与一般的判别模型做比较可能会更容易理解,即把 z z z x x x 过拟合 ,每个 ( x n , y n ) (x_n,y_n) ( x n , y n ) z n z_n z n 毫无泛化能力可言 !
那么信息瓶颈做了什么?
x x x p ( z ∣ x ) p(z|x) p ( z ∣ x ) 所有 z ∼ p ( z ∣ x ) z \sim p(z|x) z ∼ p ( z ∣ x ) 共享一个 decoder q ( y ∣ z ) q(y|z) q ( y ∣ z )
表示空间必须连续 ;
相近的 z z z 相似的语义 ;
举个例子,如果两个样本 x i , x j x_i, x_j x i , x j p ( z ∣ x i ) , p ( z ∣ x j ) p(z|x_i), p(z|x_j) p ( z ∣ x i ) , p ( z ∣ x j ) z z z q ( y ∣ z ) q(y|z) q ( y ∣ z ) 同时对多个样本都合理的输出 ;模型只能从 x x x y y y y y y
四、实验效果
略了。等读到具体论文可以补充到这。
参考资料