图论题型
10.1.1 度序列可简单图化
可简单图化的充要条件:
例题:
解法:每次度序列按非递增顺序排列,删除度最大的节点,更新其他节点的度,重新排列,继续重复上述过程。有2种不合理的情况:
(1)某次对剩下序列排序后,最大的度数(设为d1)超过了剩下的顶点数;
(2)对最大度数后面的d1个数各减1后,出现了负数。应用:Frogs’ Neighborhood
Description
未名湖附近共$N$个大小湖泊$L_1, L_2, \cdots, L_n$(其中包括未名湖),每个湖泊$L_i$里住着一只青蛙$F_i(1 \le i \le N)$。如果湖泊$L_i$和$L_j$之间有水路相连,则青蛙$F_i$和$F_j$互称为邻居。现在已知每只青蛙的邻居数目$x_1, x_2, \cdots, x_n$,请你给出每两个湖泊之间的相连关系。
Input
第一行是测试数据的组数$T(0 \le T \le 20)$。每组数据包括两行,第一行是整数$N(2 < N < 10)$,第二行是$N$个整数,$x_1, x_2,\cdots, x_n(0 \le x_i \le N)$。
Output
对输入的每组测试数据,如果不存在可能的相连关系,输出"NO"。否则输出"YES",并用$N\times N$的矩阵表示湖泊间的相邻关系,即如果湖泊$i$与湖泊$j$之间有水路相连,则第$i$行的第$j$个数字为$1$,否则为$0$。每两个数字之间输出一个空格。如果存在多种可能,只需给出一种符合条件的情形。相邻两组测试数据之间输出一个空行。
Source
参考代码
1 | |
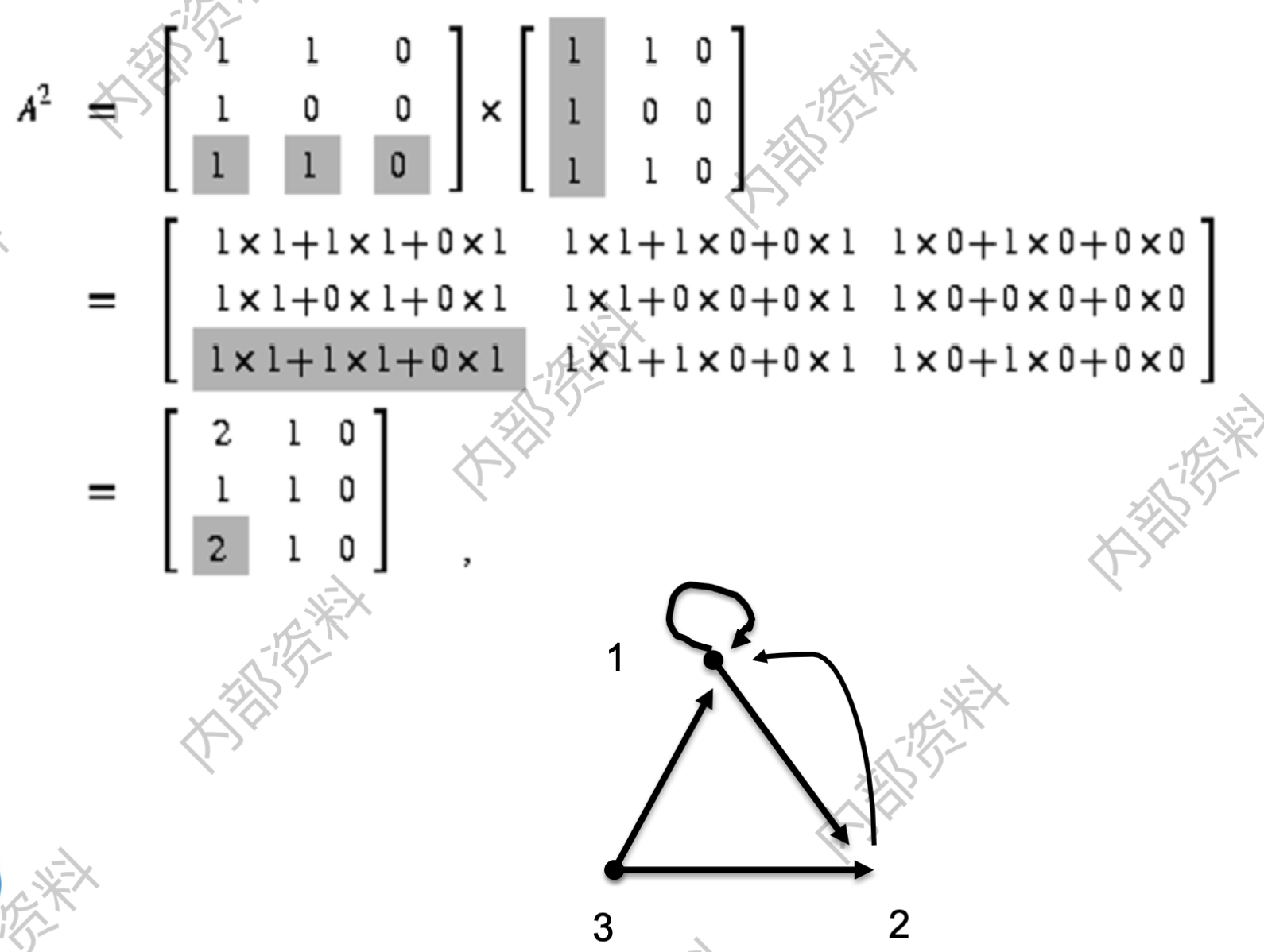
10.1.2 计算两点之间长度为k的通路数Counting Paths by Adjacency Matrices

类似求传递闭包。