平面图

一、定义

• 如果一个图能画在平面上使得它的边仅在端点相交，则称这个图为可嵌人平面的，或称为平面图。平面图G的这样一种画法称为G的一个平面嵌人。
  
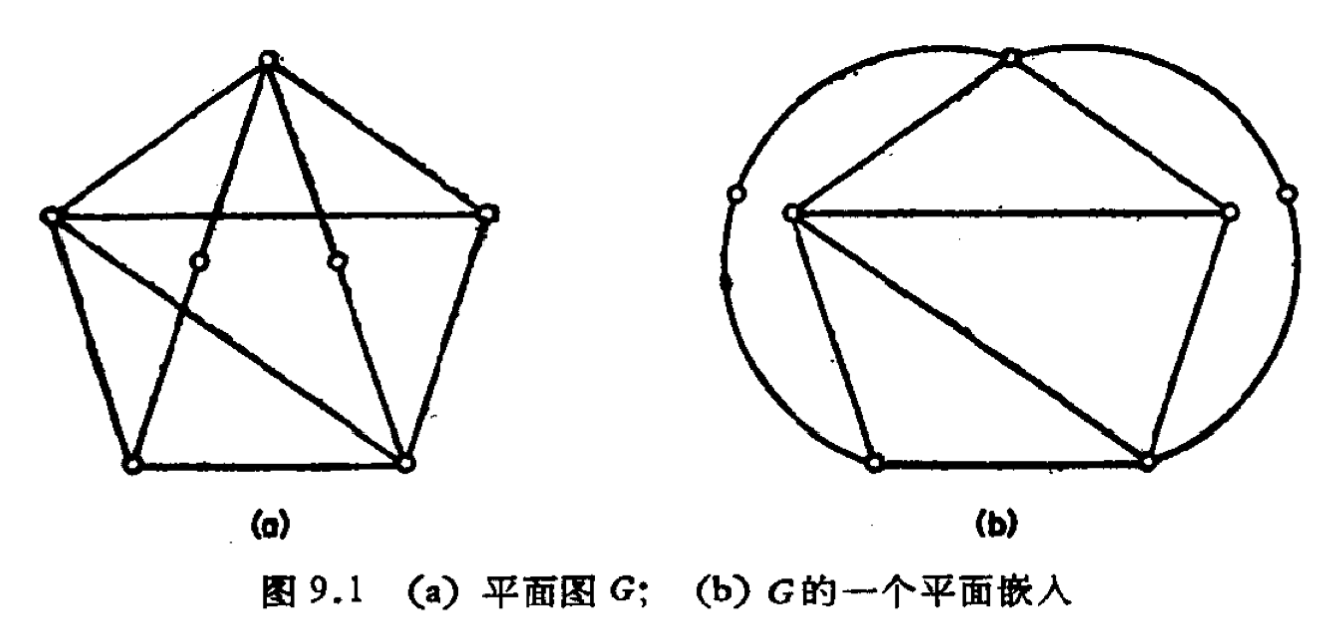
• 一个平图$G$把平面划分成若干个连通区域，这些区域的闭包称为$G$的面。面边界回路的长度称为面的次数，记为$Deg(f)$或$d(f)$。
• 每个平图恰有一个无界的面，称为外部面。

二、相关性质和定理

2.1 面的次数之和与边数关系

$\sum {d(f)} = 2\varepsilon$

2.2 Euler公式

若$G$是连通平图，则有：$\nu - \varepsilon + \phi = 2$

简单平面图存在一个度数小于5的顶点；

三、判断方法

3.1 必要条件

1. 若$G$是$v \ge 3$的简单平面图，则$\varepsilon \le 3\nu - 6$。

2. Euler公式

3.2 Kuratowski’s Theorem(库拉托夫斯基定理)

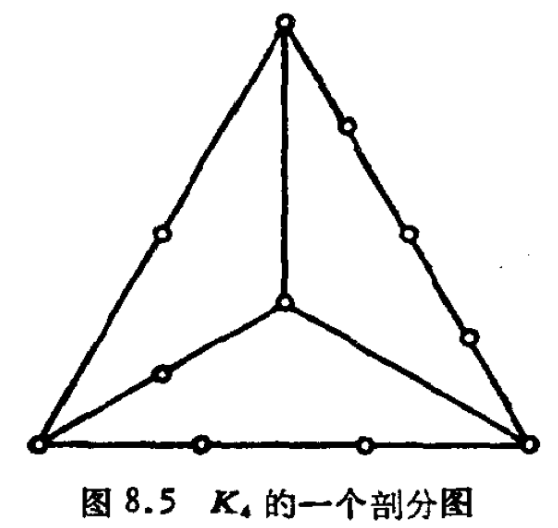
一个图是平面图当且仅当它不包含$K_{3,3}$或$K_5$的剖分图.

剖分图：把$G$的边进行一系列剖分得到的图

剖分图也可以这么理解：即用Path代替Edge。
把边$(u, v)$删除，添加一个点$w$，再添加两条边$(u,w)$和$(w, v)$，称之为初等细分；
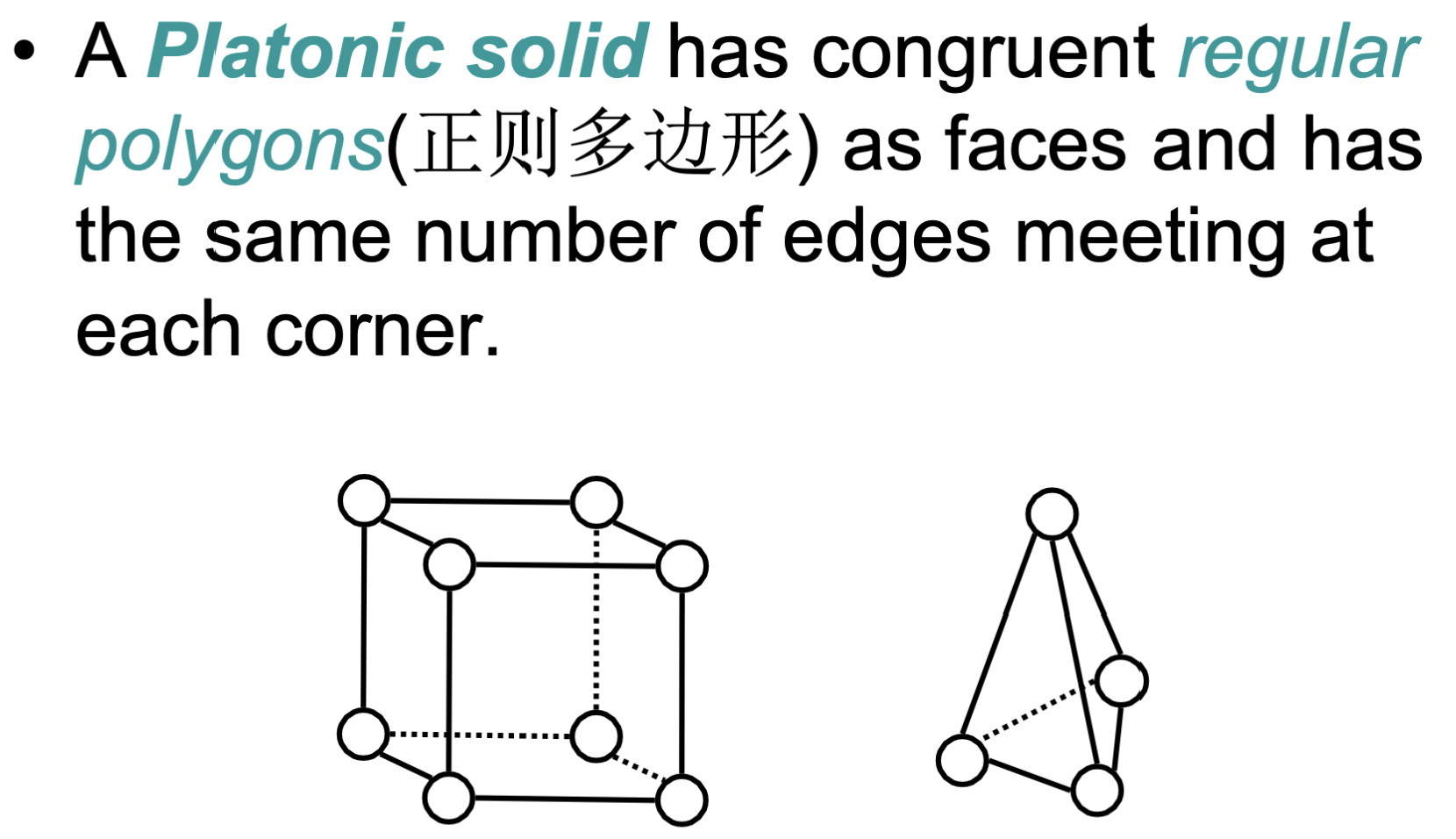
得到的新图和原图称之为是同胚(Homeomorphic)的；

Platonic Solids(柏拉图体):
顶点数、边数(棱数)、面数的关系：
其中，$v$表示顶点数，$e$表示棱数，$f$表示面数，$k$为每个顶点的出发边的数目，$l$为每个面上边的数目，$\sum deg(v) = 2e = fl = kv$.